Hinführung
Die Unterrichtsstunde ist für das Niveau der Grundschule im Fach Mathematik konzipiert und geplant. Im Mittelpunkt steht die Vermittlung von ersten geometrischen Kenntnissen mithilfe von Informatik-Tools. Der Einfluss von informatischen Medien spiegelt sich in der Verwendung des graphischen Programmierungstools „Scratch“, wie auch in der Nutzung von stromlosen Medien (siehe Abb. 3 & 5) wider. Im weiteren Verlauf werden die Ziele der Schulstunde, wie auch die zu vermittelnden Teilkompetenzen genau erläutert. Auch werden alle verwendeten Arbeitsmaterialien hier zur Verfügung gestellt.
Einstieg
Für den Einstieg wird ein Sitzkreis gebildet. Anschließend wird ein stummer Impuls gesetzt, indem Karten mit verschiedenen einfachen, geometrischen Formen und deren Bezeichnungen auf den Boden gelegt werden. Die Aufgabe der Schüler*innen ist es diese Karten zu Begriffen begründet zuzuordnen. Für den Einstieg wird ein Spiel gewählt, welches das Vorwissen der Kinder im Bezug auf geometrische Formen aktivieren soll. Das Drag-N-Drop Spiel ist auf der Webseite als H5P Element integriert. Dies soll eine mögliche Überforderung, auf Seiten der Nutzer*innen, beim Anschauen der Webseite, verhindern.
Einstieg-Zuordnungskarten-1
Abb. 1 (Zuordnung von geometrischen Figuren und deren Bezeichnungen)
Erarbeitung
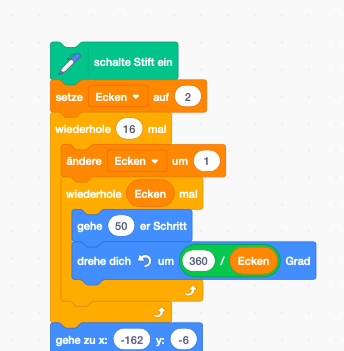
Nach der Einweisung der Schüler*innen in den folgenden Arbeitsauftrag, werden die Schüler*innen analog mit dem Arbeitsblatt (siehe Abb. 2) und Scratch ein Dreieck programmieren. Dies soll die informatischen Fähigkeiten, sowie das geometrische Verständnis für das Dreieck fördern.
AB-ProgrammablaufplanBenötigtes Vorwissen: Erste Erfahrungen in Scratch
Abb. 2 (Progammierungsplan Dreieck)
https://scratch.mit.edu/projects/687287865
Arbeitsphase
In den folgenden drei Arbeitsphasen lernen die Schüler*innen vertieft geometrische Figuren kennen. Hierzu zählen das Dreieck, das Viereck und das Fünfeck. Außerdem werden anspruchsvollere informatische Fähigkeiten benötigt. Diese werden ebenso, wie das geometrische Verständnis gefördert.
1. Arbeitsphase
In diesem Arbeitsphasen Abschnitt wird den Schüler*innen ein Link, zu Scratch, zur Verfügung gestellt, welcher von jedem Schüler*in individuell geöffnet werden muss. Auf der Programmierseite müssen die Schüler*innen in Einzelarbeit den Anweisungen der dargestellten Katze folgen.
Unterrichseinstieg_Erkennen von geometrischen Formen on Scratch (mit.edu)
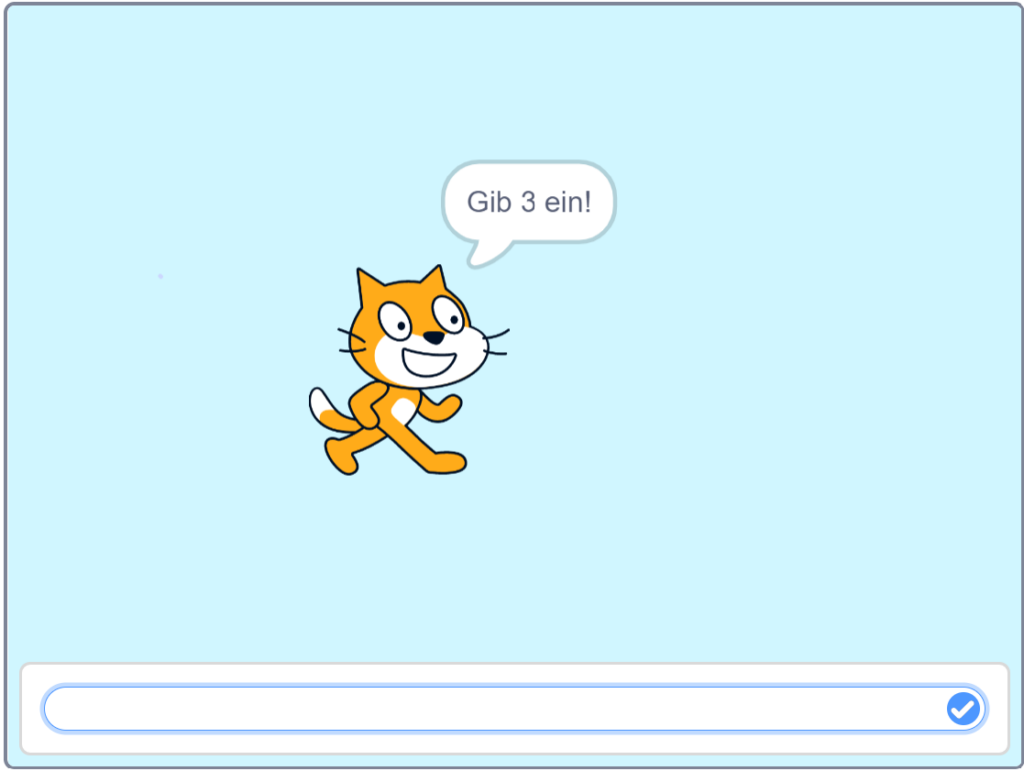
Welche Formen sind zu erkennen?
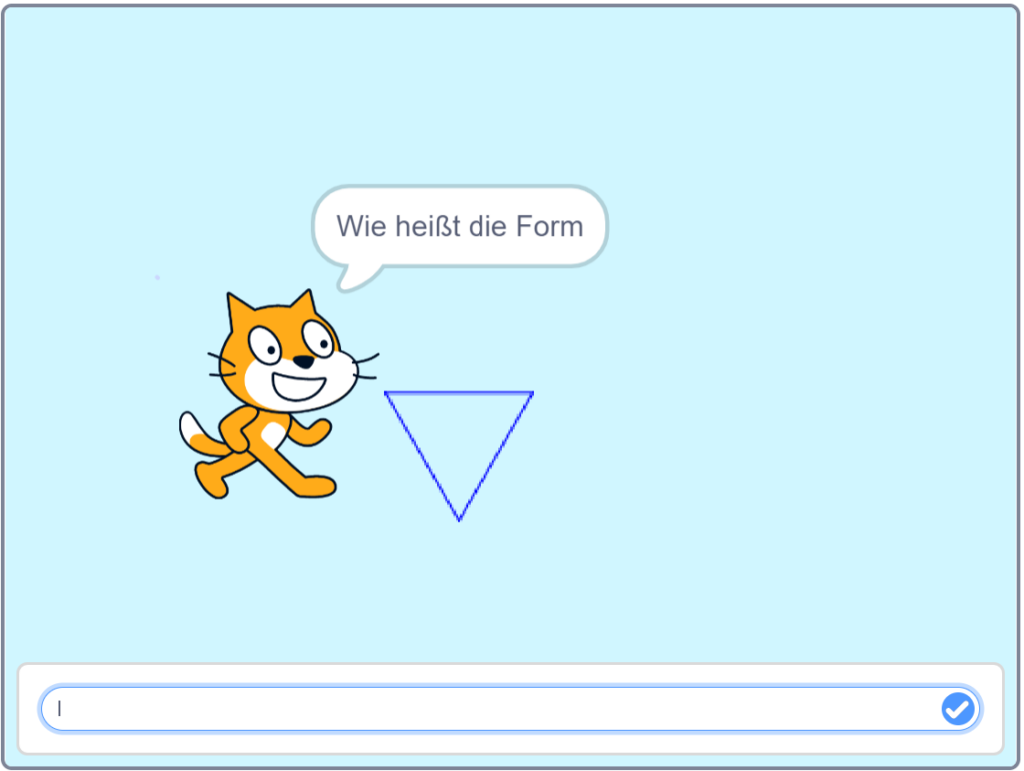
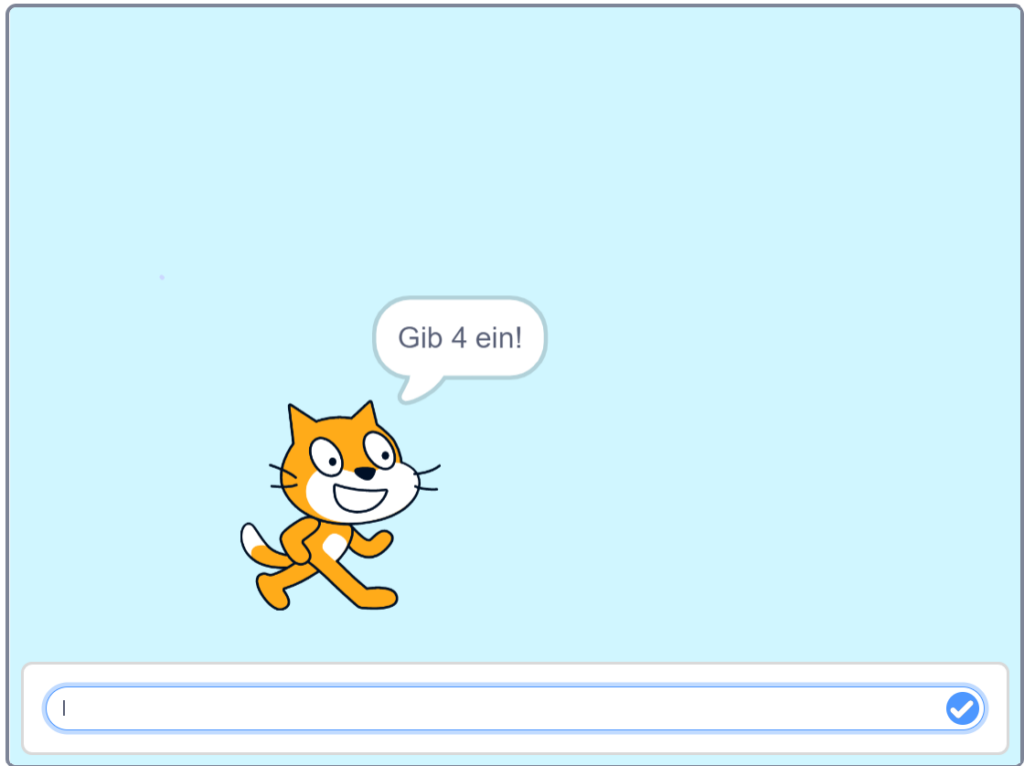
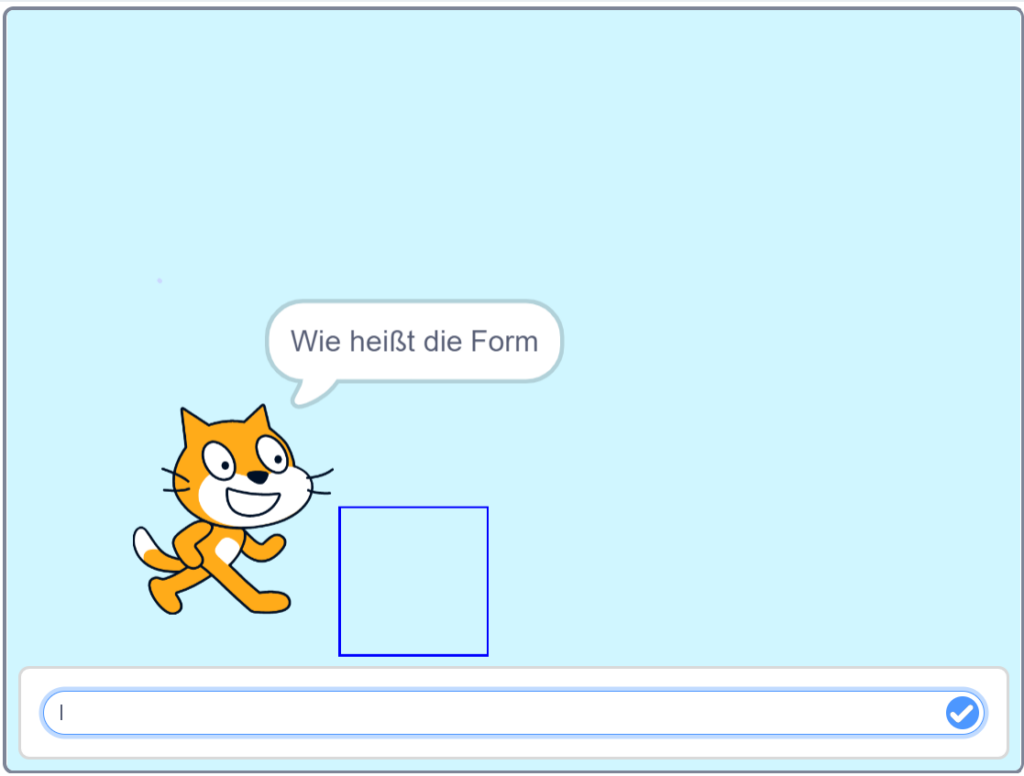
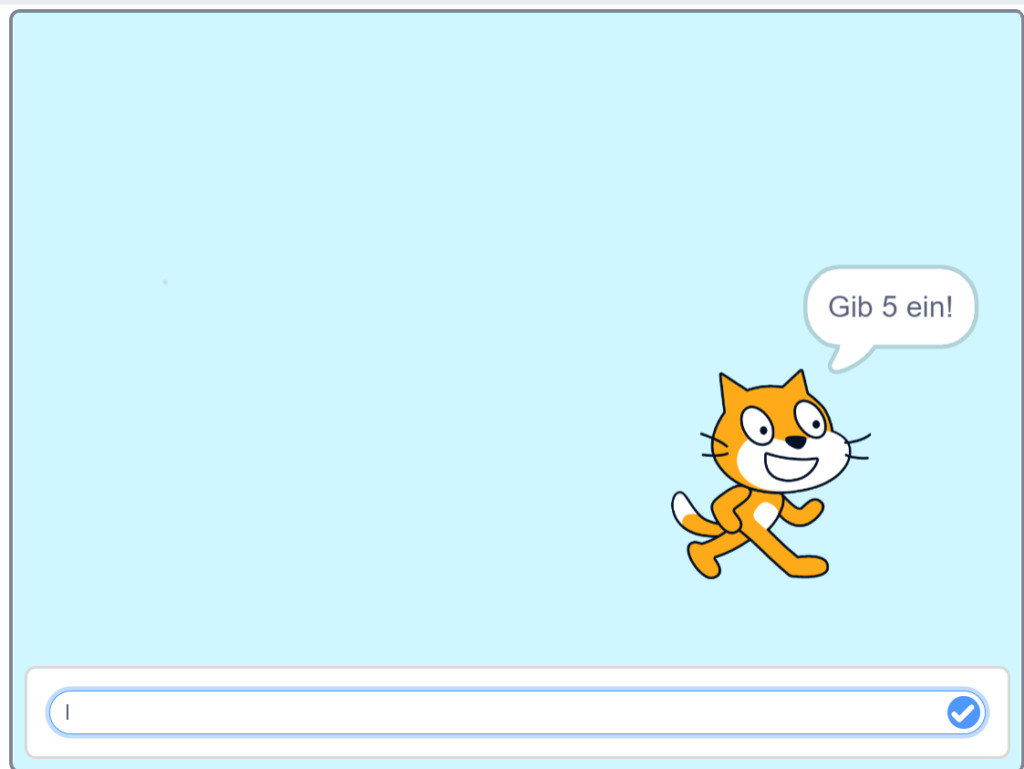
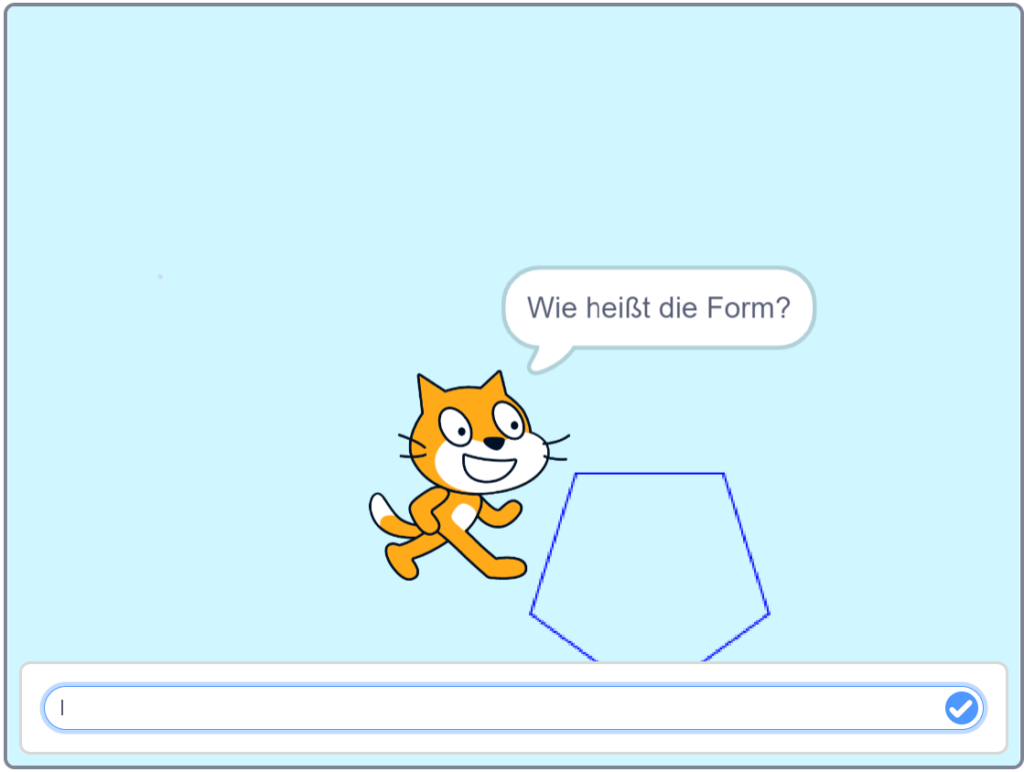
2. Arbeitsphase
In der zweiten Arbeitsphase werden Arbeitsblätter ausgeteilt auf denen sich die Codeblöcke zum Bearbeiten der dritten Arbeitsphase finden. Zunächst sollen die Schüler*innen die Blöcke so arrangieren, dass dies für sie eine geeignete Abfolge darstellt. Hier wird das Medium der Informatik ohne Strom angewandt.
Resultat
3. Arbeitsphase
Bei der dritten Arbeitsphase sollen die Schüler*innen erneut informatische Fähigkeiten in Bezug auf Scratch erwerben, indem sie, ähnlich wie bei dem Erstellen des Dreiecks, ein Viel-Eck programmieren sollen. Dies wird fähigkeitsorientiert differenziert. Erfahrene Schüler*innen dürfen ohne „Tippkarten“ (siehe Abb. 3) den Dinosaurier dazu bewegen ein Viel-Eck zu zeichnen. Unsichere Schüler*innen können sich „Tippkarten“ (siehe Abb. 3) einfordern, die das Programmieren vereinfachen.
Erinnerung: Resultat
N-Eck NICHT zusammengesetzt on Scratch (mit.edu)
AB-Programmablaufplan-neu
Tippkarten
Diese dienen zur Unterstützung bei Kindern, die ihre informatischen Fähigkeiten nicht so stark ausprägen konnten. Somit wird ein differenzierter Unterricht ermöglicht.
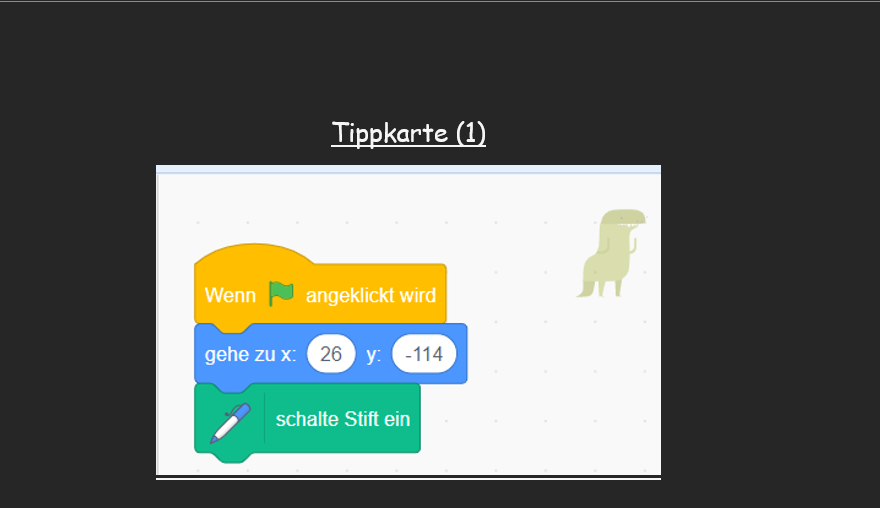
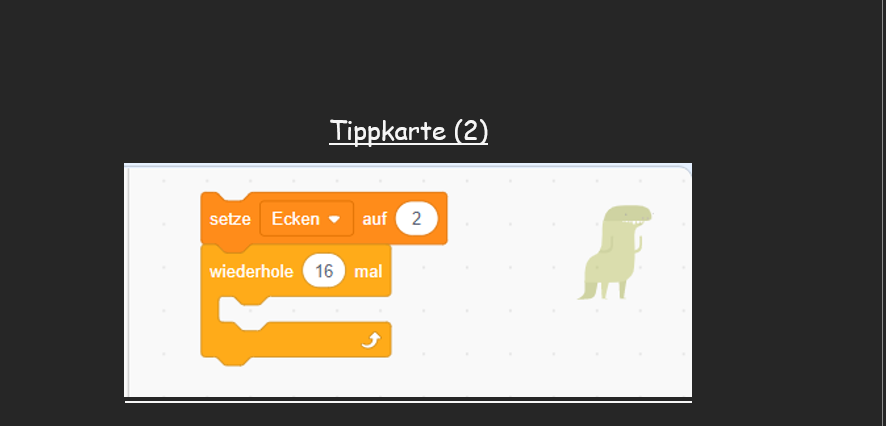
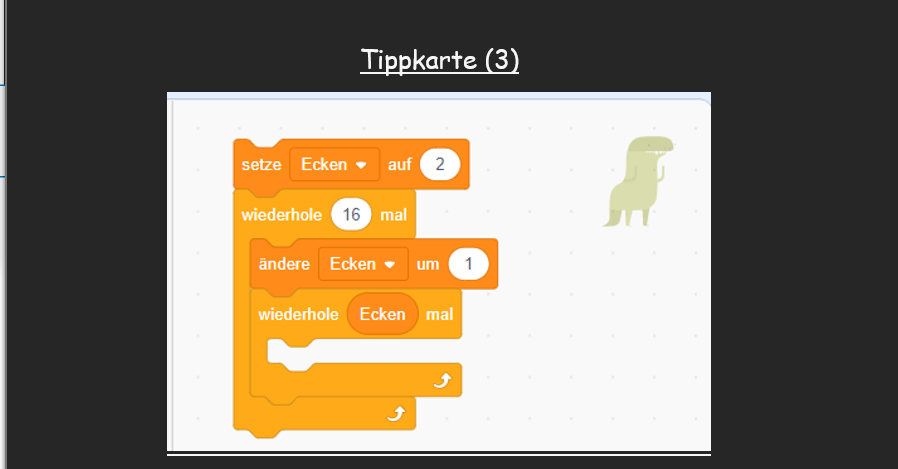
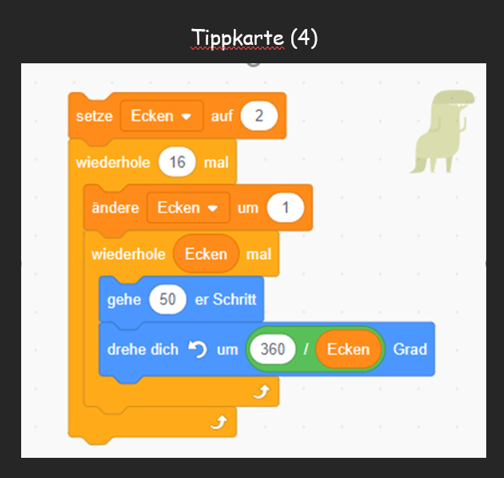
Reflexion
Bei der Reflexion sollen die Schüler*innen erkennen, dass bei dem Hinzufügen von Ecken sich eine rundere Form ergibt. Außerdem lernen die Kinder ihre Beobachtung auszuformulieren und können sich vorstellen wie ein N-Eck aussieht.
Ergebnissicherung
Für die Ergebnissicherung ist ein geometrisches Puzzle geplant.
Puzzle-geometrische-Formen-1Abb. 5 (Geometrisches Puzzle)
Hierzu finden sich die Schüler*innen in Tischgruppen zusammen. Die Tischgruppen werden von der Lehrperson zugewiesen um den Lernfluss nicht zu unterbrechen. Die Aufgabe der Schüler*innen besteht darin die zuvor von der Lehrperson ausgeschnittenen geometrischen Kärtchen zu einem geometrischen Konstrukt zusammenzufügen. Hierbei wird der Unterricht differenziert gestaltet, da jeder Schüler/ jede Schülerin nach ihren eigenen Fähigkeiten und Tempo arbeiten kann. Erfahrenere Schüler*innen können mehrere Formen bearbeiten, wobei weniger erfahrene Kinder eine geringere Anzahl an Gebilden bearbeiten kann. Diese Abschlussübung vertieft nicht nur das Verständnis gegenüber dem zuvor erarbeiteten Teilgebiet der Mathematik, sondern fördert zugleich das räumliche Vorstellungsvermögen. Des Weiteren wird das erlangte mathematische Verständnis mit informatischen Aspekten verknüpft, indem die Schüler*innen Vermutungen äußern, wie das Zusammenlegen der einzelnen Formen mit Scratch zusammenhängen könnte. Erwünscht wird das Erkennen von dem einzelnen Zusammenlegen der farblichen Kästchen zu einem Gesamtprodukt und die Verknüpfung mit der Aneinanderreihung der Programmierblöcken in Scratch. Hier fließt das Medium der „Informatik ohne Strom“ ein.
Quelle: Figuren zusammensetzen – MEDBREAKER (medat-vorbereitung.at) [Stand: 12.05.222 11:11 Uhr]
Zusätzliche Anmerkungen
Für die Unterichtsstunde wurden folgende Teilkompetenzen formuliert.
- Die Schüler*innen erkennen geometrische Grundformen und benennen diese, indem sie eine Zuordnung vornehmen.
- Die Schüler*innen erkennen den Zusammenhang zwischen geometrischen Grundformen, indem sie die Transformation der Formen durch das Hinzufügen von Ecken nachvollziehen.
- Die Schüler*innen festigen die Begriffe und Eigenschaften geometrischer Figuren, indem sie sie auf ikonischer, symbolischer und enaktiver Ebene erfassen.
- Die Schüler*innen erwerben das Wissen, das eine geometrische Figur aus weiteren geometrischen Figuren zusammengesetzt werden kann.
- Die Schüler*innen erweitern ihre Medienkompetenz, indem sie analoge Darstellungen in digitale Darstellungen übertragen.
- Die Schüler*innen erweitern ihre Fähigkeit digitale Werkzeuge zu verwenden, indem sie algorithmische Grundbausteine entsprechend der Anweisungen anordnen und verändern.
- Die Schüler*innen kommunizieren über informatische Inhalte und Zusammenhänge, indem sie algorithmische Darstellungen versprachlichen.
- Die Schüler*innen tauschen sich über Denkprozesse und Vorgehensweisen aus, indem sie mit ihrem Partner geeignete Lösungswege für die Programmierung finden.
Abb. 6 (Unterrichtsverlaufsplanung)
Persönliche Reflexion
Persönliche Reflexion
Die zugehörige Unterrichtsstunde wurde im Rahmen einer Hybridveranstaltung durchgeführt, wodurch in der Durchführung unerwartete Probleme entstanden. Die Studierenden wurden bei der dritten Arbeitsphase von der Lehrperson darauf hingewiesen, dass sich die Tippkarten auf der WordPress Seite befinden. Dies sollte dazu dienen, dass auch die Online-Teilnehmer einen Zugang zu den Tippkarten erhalten. Leider hat es vor allem bei den Präsenzteilnehmern dafür gesorgt, dass diese sich alleine auf die Arbeitsanweisung konzentriert haben und sich somit kein Diskurs zwischen Studierenden und Lehrperson ergab. Die zuvor ausgedruckten Tippkarten wurden daher nicht von den Studierenden verwendet. Außerdem wurde bei der Erstellung der WordPress Seite nicht bedacht, dass das Anzeigen von Lösungen dazu führt, dass die Studierenden diese zuvor entdecken und kein Lernprozess stattfinden kann. Die Lösung für das Codieren des Dinos findet sich unter Abbildung 3 „Codierungsplan zum Ausschneiden und eigenständigem Zusammensetzen“. Eine mögliche Lösung wäre eine H5P Datei, bei der die Codierungsblöcke aneinander gezogen werden können. Somit wäre eine Eigenüberprüfung möglich gewesen.
Des Weiteren erhielten wir negatives Feedback bezüglich der Präsentation der Unterrichtsstunde. Da der Unterricht für eine Grundschulklasse geplant war, konnten sich die Studierenden nur schwer an die „Du-Sprachweise“ gewöhnen. Ebenso wären an einigen Stellen genauere Anweisungen zu wählen gewesen. Besonders hervorgehoben wurde dabei die erste Arbeitsphase und der Einstieg. Die Lehrperson hätte vertieft auf die Aufgabenstellung eingehen müssen. Hinzukommt, dass ein verstärktes Erfragen von potenziellen Problemen der Studierenden, diese hätte lösen können. Beim Einstieg wurde die didaktische Methode des stillen Impulses angewandt. Dieser hat unter den Studierenden jedoch für Verwirrung gesorgt, da diese Methode ihnen nicht bekannt war. Eine vorzeitige Erläuterung des stillen Impulses hätte den Einstieg einfacher gestaltet.
Ein weiterer, häufig angemerkter Kritikpunkt war das Nutzen des Wortes „Viereck“ als Äquivalent zu einem Quadrat ohne zuvor erläutert zu haben, dass ein Viereck gleichzusetzen ist mit dem programmierten Quadrat (siehe hierzu Unterrichtseinstieg ‚Erkennen von geometrischen Formen on Scratch‘). Dies könnte behoben werden, indem in das Scratch Programm ein oder-Baustein eingefügt wird, sodass das Programm die Wörter „Viereck“ und „Quadrat“ als richtig akzeptiert. Auch eine genaue Erläuterung, dass ein Quadrat und ein Rechteck in die Kategorie des Vierecks fallen hätte für weniger Verwirrung gesorgt. Ebenso hätte bei den Zuordnungskarten zum Einstieg der Unterrichtsstunde das Viereck mit dem Quadrat und Rechteck verknüpft werden können. Ein weiteres Problem dieses Programms hat sich bei dem Zeichnen der Katze gezeigt. Hier wurde die Katze so programmiert, dass diese nach dem Zeichnen einer Form zu einer zufälligen Position springt, um dort die nächste Figur zu zeichnen. Leider bedeutet dies, dass die Katze häufig hinter dem Bildschirmrand verwindet und so die erstellte Form kaum ersichtlich ist. Durch das Einhalten einer Position der Katze und dem Löschen der vorherigen Figur hätte dies vermieden werden können.
Trotz positivem Feedback zu der WordPress Seite hat sich hier ein Fehler eingeschlichen, der bei der Überarbeitung der persönlichen Reflexion korrigiert wurde. Alle beiden Programmablaufpläne, für den Einstieg und die Arbeitsphase, wurden in einem gemeinsamen PDF-Feld dargestellt. Hinzukommt, dass der Programmablaufplan für die erst später relevante, dritte Arbeitsphase zuerst angezeigt wurde. Dieses organisatorische Missgeschick wurde, wie oben erwähnt, behoben.
Durchweg empfanden beide Präsentierende das Feedback als positiv. Häufig wurde positiv angemerkt, dass die Unterrichtsstunde abwechslungsreich gestaltet wurde und eine Methodenvielfalt gegeben war. Hier wurde besonders der Wechsel zwischen digitalen Medien (Scratch, WordPress, H5P etc.) und Präsenzmedien (Zusammenlegen der geometrischen Formen in der Ergebnissicherung & Sitzkreis mit Karten-Zuordnen-Spiel) hervorgehoben.
Fazit
Das Planen der Unterrichtsstunde mit dem Einfluss von digitalen Methoden, wie beispielsweise Scratch, erwies sich als ungewohnt. Welches Thema ist für Grundschulkinder zumutbar? In welchem Fach bietet sich die grafische Programmiersprache am besten an? Wie können informatische und nicht informatische Aspekt ein einer Unterrichtsstunde passend verknüpft werden? Nach der Themenfindung konnte sich kreativ betätigt werden, in wieweit man Scratch zur Themenvermittlung nutzen kann. Nach einigen Fehlprogrammierungen wurde ein gewisses Gespür für Scratch entwickelt. Dies ermöglichte eine Anpassung des Programms für das Niveau der Grundschule. Bei weiteren verknüpften Unterrichtseinheiten mit beispielsweise Scratch könnten sich Schüler*innen eigene Programme entwickeln, die das Verständnis von geometrischen Formen (wie in dieser geplanten Unterrichtsstunde) vertiefen.
Durch diese Veranstaltung wurde ein wichtiger Einblick in die informatischen Möglichkeiten in der (Grund-)schule ermöglicht. Auch die Vorteile von fächerübergreifendem Informatikunterricht wurde verdeutlicht. Gleichzeitig wurde eine kreative und eigenständige Erarbeitung von Themen gefördert und unterstützt. Abschließend anzumerken ist, dass die Veranstaltung den Unterrichtshorizont erweitern konnte, womit neue gestalterische Aspekte, für zu planende Unterrichtsstunden, offengelegt wurden.